কোনো সমীকরণের চলকের সর্বোচ্চ ঘাতকে সমীকরণটির ঘাত বলে। যে সমীকরণে চলকের সর্বোচ্চ ঘাত 2 তাকে দ্বিঘাত সমীকরণ বলে।
ax2+bx+c=0 [যেখানে, a, b,c ধ্রুবক এবং a≠0] আকারের সমীকরণকে এক চলক বিশিষ্ট দ্বিঘাত সমীকরণ(Quadratic Equation) বলা হয়। দ্বিঘাত সমীকরণের বামপক্ষ একটি দ্বিঘাত বহুপদী। সমীকরণের ডানপক্ষ শূন্য ধরা হয়।
x2+5x+6=0
y2-y=12
4x2-2x=3-6x
সমীকরণগুলোর প্রত্যেকটির ঘাত 2; এগুলো এক চলকবিশিষ্ট দ্বিঘাত সমীকরণ।
দ্বিঘাত সমীকরণের মূল নির্ণয়ের সূত্র
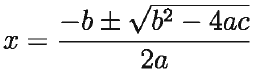
নিশ্চায়কের অবস্থাভেদে দ্বিঘাত সমীকরণের মূলদ্বয়ের ধরন ও প্রকৃতি
ধরি a, b, c মূলদ সংখ্যা তাহলে,
ক) b2-4ac>0 এবং পূর্ণবর্গ হলে সমীকরণটির মূলদ্বয় বাস্তব, অসমান ও মূলদ হবে।
খ) b2-4ac>0 কিন্তু পূর্ণবর্গ না হলে সমীকরণটির মূলদ্বয় বাস্তব, অসমান ও অমূলদ হবে।
গ) b2-4ac=0 হলে সমীকরণটির মূলদ্বয় বাস্তব ও পরস্পর সমান হবে, এক্ষেত্রে x=-b/2a
ঘ) b2-4ac<0 অর্থাৎ ঋণাত্মক হলে সমীকরণটির বাস্তব মূল নাই।
- দ্বিঘাত সমীকরণটির মূলদ্বয় জানা থাকলে সমীকরণটি হবে: x2-(α+β)x+αβ=0
- ax2+bx+c=0 দ্বিঘাত সমীকরণে b=0 হলে মূল দুইটির মান সমান কিন্তু বিপরীত চিহ্নযুক্ত হবে।